ELEMENTAARTEADMISI LAUSE- JA PREDIKAATARVUTUSEST

---

Loogikaõpiku esilehekülg näeb välja umbes selline.

Lausearvutuse tehted on binaarsed ja unaarsed.

Binaarsed tehted seovad kaht lauset ja tehte tõeväärtus sõltub mõlema komponentlause tõeväärtusest. Binaarsete tehetena võib printsiibis käsitada kahendmuutuja mistahes funktsioone, kuid loogikatehetena on tuntuimad järgmised:

1) konjunktsioon;
2) disjunktsioon;
3) ekvivalents;
4) alternatiivne eitus e. nn. Shefferi joon;
5) implikatsioon.

Unaarseid, ühe muutuja tõeväärtusest sõltuvaid tehteid on üks — eitus.

Esimese nelja tehte juures on komponentlausete järjekord vaba, implikatsiooni juures fikseeritud: meie näites on X implikatsiooni eesliige e. antetsedent, Y tagaliige e. konsekvent.

(Seejärel tehakse juttu samaselt tõestest valemitest, loogilisest samaväärsusest, konjunktsiooni ja disjunktsiooni kommutatiivsusest, assotsiatiivsusest ja distributiivsusest jne.)

Lausearvutusest mitmeti peenem süsteem on predikaatarvutus. Siin tungitakse juba sedavõrd lause sisusse, et lause jagatakse kaheks komponendiks: temaatilist poolt märkivaks indiviidiks (e. argumendiks) ning predikaadiks. Eristatakse nagu lausearvutuseski konstante ja muutujaid: on

individuaalkonstandid (nt. a, b, c),
individuaalmuutujad (nt. x, y, z),
predikaatkonstandid (nt. P, Q, R) ja
predikaatmuutujad (nt. F, G, H).

Predikaatarvutuses on võimalik eristada ka üldistavaid väiteid mitteüldistavaist. See toimub sümbolite abil, mida nimetatakse kvantoriteks.
Sümbolit nimetatakse üldisuse kvantoriks ning väljend x (Fx) tähendab umbes: 'igal (teatud piirkonnast) indiviidil x on predikaat F' ehk 'kõik x-id on F' vmt.
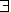Sümbol on olemasolu kvantor ja väljend x (Fx) tähendab umbes: 'eksisteerib indiviid x, millel on predikaat F' ehk 'mõned x-id on F' vmt.